#Technomous

所谓数学家，就是能够发现定理之间相似之处的人。
好的数学家能够看到证明之间的相似。
最优秀的数学家则能够看到理论之间的相似。
可以想象，终极的数学家应该能够看到相似之间的相似。

——斯特凡·巴拿赫（Stefan Banach，1892–1945）

凡物无成与毁，复通为一。唯达者知通为一。

——庄子

你取来一杯黑咖啡，在电脑前坐下来，将准备好的牛奶倒进咖啡，然后用勺子慢慢搅拌，咖啡很快就从黑白分明变成了棕色，散发出温和的香味。然后你在电脑上看到这样的文字：

假设X是一个上密度为正的自然数集合，那么对于所有的正整数k，在X中都存在一个长度为k的等差数列。

这似乎跟你和你的咖啡毫不相干，但阿贝尔奖，也可以说是数学界的终身成就奖，今年的两位得主希勒尔·弗斯滕伯格（Hillel Furstenberg）和格里戈里·马尔古利斯（Grigory Margulis）获奖的原因，正是他们看到了搅拌咖啡和代数、数论以及组合的某些问题之间的相似性，并由此解决了许多问题，发展出了新的数学分支。

但在具体解释两位获奖者的工作之前，我们先来考虑一个问题：为什么将加了牛奶的咖啡搅拌之后，它就会慢慢变得均匀？

结局与路线

这个问题似乎太简单了，本来分开的东西，搅拌一下就会混合起来，咖啡是这样，颜料也是这样，这都是天经地义的事情，还用问吗？

问题在于，这并不是天经地义。比如说水和油，如果随便搅拌一下的话，只消静置几分钟，水和油就又分离开来了。虽然在特定的条件下，油可以分为极其细小的油滴悬浮在水中，与水均匀混合，比如说牛奶就是这样，但这种状态并不是绝对稳定的。比如说，拿起半瓶牛奶用力摇晃十几分钟后，你就会发现牛奶分成了固体和液体两部分，固体部分就是奶油，也就是原来悬浮着的油滴。

那么，为什么牛奶和咖啡可以轻易混合，但水和油却不行呢？物理中的热力学给出了答案：水分子和油脂分子非常不喜欢靠近对方，硬要混合它们就需要很大的能量，而如果顺其自然的话，假以时日它们会逐步到达能量最低的地方，也就是水油分离。牛奶和咖啡的分子没有这个问题，所以能够均匀混合。

这是个很好的解释，但并没有回答我们一开始的问题。热力学告诉我们咖啡和牛奶能够混合均匀，但却没有告诉我们搅拌在其中扮演了什么角色。热力学能告诉我们结局，但对于如何到达这个终点却是无可奉告。就像人终有一死，这是热力学的答案，但我们更关心的是这个人经历了什么，是重于泰山还是轻于鸿毛。能告诉我们这些的，是物理的另一门分支，也就是动力学。

动力学研究脱胎于庞加莱对天体力学的研究。自从牛顿发现天体流转和苹果落地同样遵循万有引力的同一套微分方程之后，人们就开始利用微积分的语言来描述和研究行星的运动，也依此发现了海王星。自此之后，数学家将同样的一套方法论应用到不同的物理体系甚至数学体系中，也就形成了一门新的学科。

动力学研究的，就是物理系统怎么样从一种状态演变为另一种状态。被搅拌着的咖啡和牛奶构成了一个所谓的“动力系统”，而动力学研究的，则是各种各样的动力系统如何随时间而演变。无论是钟摆来回摇动，还是气象风起云涌，甚至连太阳系的运转，都可以看成某种动力系统。而对动力系统的研究，随着研究对象越来越多，也逐渐变得越来越抽象，最后演变为一门独立的数学分支。

飘摇的轨迹

为了研究不同的动力系统，数学家引入了状态空间的概念，在物理学中也叫相空间，它是一个抽象的几何空间，其中每个点都对应于动力系统的某个特定的状态。比如说，如果考虑太阳系行星这个动力系统的话，可以固定太阳的位置为原点，而八大行星各自的位置和速度就组成了动力系统的状态。每个行星的位置和速度都分别需要3个数来描述，合起来的话，要描述太阳系行星这个动力系统就需要48个变量，而它对应的状态空间也就是一个48维的空间。动力系统随时间的演变就相当于状态空间中点的轨迹，而动力系统理论研究的就是这些轨迹的行为。

不同的动力系统，对应的状态空间中也有着各种各样的轨迹。比如说太阳系对应的状态空间，有的轨迹经过一段时间就会一去不复返，这就意味着某个行星永远地离开了我们；有的轨迹是闭合的，一次又一次地重复自身，形成动态稳定的体系；有的轨迹虽然不会完全重复自身，但却会无限靠近某条闭合的轨道；有的轨迹却更加任性妄为，行为捉摸不定，但却像被某种奇异的力量吸引着，永远不会远走高飞。可以说，这些轨迹就决定了动力系统的性质，所以动力系统理论的研究目的之一，就是刻画这些轨迹的性质以及它们之间的关系，还有确定某个特定的状态会遵循什么样的轨迹等等。

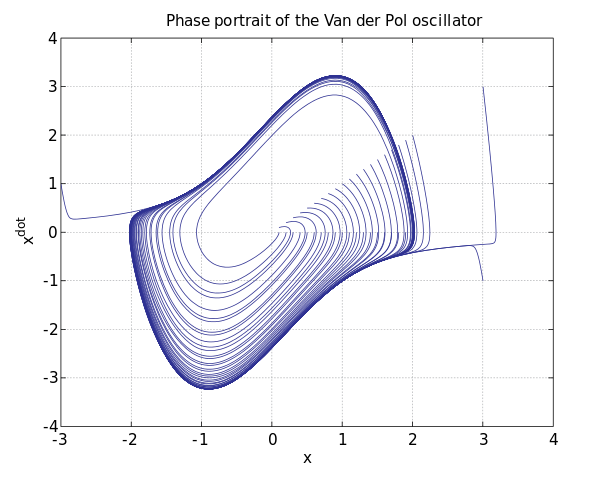
因为动力系统发源于物理学，所以人们最初研究的那些动力系统，比如星体和天气，都遵循着刻画物理规律的微分方程，对其的研究也紧紧遵循着数学分析的传统，其中的重镇就是俄国数学家亚历山大·李雅普诺夫，他对于连续动力系统中轨迹稳定性的判定有着极为重要的贡献。此外，数学家也意识到，有时候我们并不需要知道整个系统在任何时间的行为，而只需要知道在某些特定的时间间隔中系统的行为。由此得到的就是离散动力系统的概念，其中连续的时间变成了离散的时刻，而动力系统本身就决定了这个时刻的状态会如何变换成下一个时刻的状态。

但随着对动力系统研究的深入，人们发现了那些捉摸不定但却永不远离的轨迹，只要它们的初始状态有一丝一毫的偏离，经过一段时间的演化，它们就会踏上完全不同的道路。这就是混沌现象，而对这种现象的研究也已经发展成混沌理论这一独立的学科，它与概率论、分形都有密切的关系。同时，随着数学家研究的动力系统越来越复杂，他们发现确定性的微分方程似乎已经落后于时代，反而是描述随机性的概率论和描述一般空间的拓扑学更加符合他们的需要。于是，动力系统的研究方法就慢慢转向概率以及拓扑，也就此取得了更大的成果，也由此扩展到了更为广泛的对象，不一定是连续的空间，也可以是离散的对象。这就给弗斯滕伯格和马尔古利斯的工作埋下了伏笔。

走遍天下

让我们回到咖啡的例子。之前说到，热力学说明咖啡和牛奶组成的体系最终会到达能量最低的状态，但其实牛奶刚刚倒进咖啡之后，它们的能量就已经是最低的了！也就是说，热力学并没有说明为什么在搅拌之后两者会混合起来而不是仍然分离。

如果你熟悉热力学，你可能会说这就是热力学第二定律的结论，因为体系会停留在熵最大的宏观状态，也就是对应微观状态数最多的宏观状态。对于咖啡和牛奶来说，就是完全混合的状态。此话不假，但实际上正是热力学第二定律包含了一个隐含的假设：体系处于能量相同的任意微观状态的可能性都是相同的。这个假设被称为遍历假设，“遍历”的意思就是体系可以经历所有状态，而且这些状态对它来说都是平等的。遍历假设自然可以推出热力学第二定律，但在动力学上却并非显然正确，因为完全有可能存在某个状态永远不能达到。于是，想办法证明某种类似的结论就成了数学家心头的一大问题。

把牛奶加入咖啡中，搅拌之后牛奶还是那么多，只不过分散在了整杯咖啡之中，搅拌的操作不会改变牛奶的多寡。许多动力系统也是如此：我们可以在状态空间中定义某种“容积”的概念，用术语来说就是测度，使得一组占据一定容积的系统状态，无论经过多少时间，仍会占据着相同的容积。这种动力系统被称为保测动力系统，“保测”的意思就是“保持测度”。

庞加莱在研究天体力学时就已经注意到任何由常微分方程定义的动力系统都满足这一条件，也就是说，所有通过经典力学构建的动力系统都是保测动力系统。同时，它们因此有着特殊的性质：如果系统中没有任何轨迹会无限远离的话，那么从任何初始状态出发的轨迹，假以时日，即使不能回到初始状态，也可以到达离它要多近有多近的某个状态。这就是庞加莱复现定理。这个定理也被另一位数学家策梅洛用于质疑热力学第二定律：如果系统总是能返回初始状态的话，那么混合好的咖啡和牛奶也终有一天会重新泾渭分明，这似乎正是热力学第二定律所禁止的。

幸而，正如热力学只告诉我们最终结局，庞加莱复现定理也只告诉我们最终会回到某个非常靠近初始状态的地方，但没有说清楚需要多少时间。通过仔细计算，我们能够得到大概所需的时间，也就是所谓的庞加莱复现时间。对于一杯加了牛奶的咖啡来说，这个时间比宇宙的年龄还要长得多，这就保住了热力学第二定律作为经验法则的地位。但这也意味着，如果我们希望考虑系统长期的变化，也许不应该着眼于单个时刻的状态，而更应该考虑长期变化的平均值。

在二十世纪三十年代，冯诺依曼和伯克霍夫等人各自在这个方向上的努力最终结出了成果。他们证明了所谓的“遍历定理”：假设由常微分方程定义的动力系统满足某些假设，那么给定状态空间中的某个领域，从任意状态出发的演化过程通过这个领域的时间比例几乎必然会趋近于领域在整个状态空间中所占据的空间比例。比如说，如果搅拌的方法满足某些假设，那么即使我们不去追踪咖啡杯里牛奶的某个液滴划过的轨迹，也可以确定它大概有一半时间会呆在咖啡杯左半边。这就相当于证明了遍历假设在平均意义上是正确的，于是热力学第二定律也是如此。

那么，遍历定理中的“某些假设”到底是什么呢？

说起来也简单。在状态空间中，我们考虑某个容积不为零，但严格小于整个空间的区域。直觉上来说，如果所有能够到达这个区域的状态恰好就是这个区域内的所有状态的话，那么遍历假设显然就不成立，因为区域以外的大量状态无法进入这一区域。神奇的是，只要假定这种区域不存在，遍历定理就必然成立。满足这个条件的保测动力系统就是所谓的遍历系统，而遍历理论就是对遍历系统的研究。

伯克霍夫也意识到，他的遍历定理实际上并没有局限于常微分方程定义的动力系统，而是应该对于其他遍历系统也成立。后来的研究者沿着这个方向，将遍历定理进行了大量的推广。随着研究的逐渐深入，人们意识到，虽然保测动力系统脱胎于微分方程描述的物理系统，但它的定义只牵涉到状态空间上的测度。也就是说，保测动力系统系统实际上相当于某个测度空间上的保测变换，正是这个保测变换让我们能从一个状态达到下一个状态，而遍历系统所需的条件也能完全用测度的语言来描述。

所以说，遍历系统的本质在于测度，而具体的状态空间到底表示什么，是整个系统的状态还是牛奶液滴的位置，这都只是表象，可以忽略的表象。正因为遍历系统的本质在于测度和保测变换，所以即使遍历系统本身没有包含任何不确定性，但遍历理论与同样建基于测度的概率论仍然有着许多共通之处。这两个领域中的研究互相渗透，已经得到了丰硕的成果。

但遍历理论和概率论毕竟仍然属于广义上的分析，它们与广义上的代数似乎相差甚远。想必任何学过大学数学课程的人都会感觉微积分与线性代数就像两个完全不同的世界。弗斯滕伯格和马尔古利斯的贡献，就在于他们借助遍历系统本身的抽象性，成功跨越了分析和代数之间的鸿沟，将遍历理论的方法应用到了代数和组合的广泛领域中，得到了大量的成果，开创了全新的领域。

弗斯滕伯格：整数中的遍历系统

弗斯滕伯格出生在1935年的德国柏林。对于一名犹太人来说，这个时机实在太坏。他可能也不太记得在德国的生活，因为在1939年的水晶之夜之后，为了活命，他父母就带着一家人逃到了美国。颠沛流离之后接下来的并不是好日子，弗斯滕伯格的父亲去世之后，他们一家的生活过得更为拮据。但这并没有阻碍弗斯滕伯格求学的脚步。他就读了专门为犹太人开设的宗教学校，然后升入了当地的大学。就在那里他接触到了数学的美，并就此走上了数学的道路。

在大学的期间，他就已经在数学方面崭露头角，因为利用拓扑的语言证明了素数有无限个而小有名气。这也许也预示了他能在不同数学分支之间看到相似性的能力。之后他到了普林斯顿大学就读博士，博士导师是同样由德国逃出来的博赫纳（Salomon Bochner）。当时博赫纳正在深入研究概率，而弗斯滕伯格的博士论文，题为《预测理论》（Prediction Theory），自然也是有关概率的。这篇博士论文讲述了对时间序列进行预测的理论，其中也牵涉到遍历理论。对于这篇论文的水平，某位评委的评语是“这是一篇具有高度原创性的第一流博士论文，涉及的课题也相当困难”。

博士毕业之后，弗斯滕伯格开始尝试将概率论的方法应用到别的数学对象之中。他通过对于随机矩阵乘积的研究，开始探索所谓“半单李群”这一类代数对象的结构，并且在一系列论文中逐步明晰定义了所谓的“弗斯滕伯格边界”，用以刻画半单李群上的调和函数。他的这项工作利用概率论的工具剖析了某些群的结构，即使这些结构与随机性毫无瓜葛。这一跨界的工作也对相关的代数研究产生了巨大的影响。

这一系列论文之后，弗斯滕伯格名声大噪，很快就得到了美国明尼苏达大学的教授职位。但此后不久，他就离开美国移居以色列，并在这个犹太人魂牵梦萦的“应许之地”扎下了根。在那里，他开始尝试继续钻研遍历理论，提出了不少重要的概念与猜想。比如说，通过类比整数之间互质的关系，弗斯滕伯格提出了遍历系统之间的“不相交性”（disjointness）。这个概念相当自然，但人们发现其实它也极为深刻，在分形几何、信号处理等领域都有着重要的应用。

但弗斯滕伯格最激动人心，大概也是最容易解释的工作还在后头。在他就职的耶路撒冷希伯来大学，经常有不同领域的数学家来做讲座。有一次，一位访客做了一个关于组合数论的报告，其中提到了当时刚刚被塞迈雷迪（Szemerédi Endre）证明的一个精彩定理。假设有一个整数的集合A，如果无论取多大的正整数n，都有一个比它更大的正整数N，使得在-N到N之间的整数至少有某个固定的比例包含在集合A中，那么A就必定包含任意长度的等差数列。用数学术语来说，就是拥有正上密度的整数集合A必然包含任意长度的等差数列。

这是个奇妙的结果。我们对集合A的要求相当弱，只要不算太稀疏，满足这个条件的集合A可以随意包含任何元素，自然也可能混乱得毫无章法。但无论集合A多么混乱，只要它的上密度为正，那么我们必定可以在这种混乱中找到某种结构，在这里就是要多长有多长的等差数列！这种断言我们必定能在混乱中找到结构的定理，属于所谓“拉姆齐理论”的范畴，它的研究牵涉到组合数学和数理逻辑，其中有着许多困难的问题，而这个后来被命名为塞迈雷迪定理的结论也是其中之一。

当时塞迈雷迪对塞迈雷迪定理的证明惊动一时，不仅是因为定理本身的难度，还因为塞迈雷迪在证明中提出了一个重要的引理，后来又将其推广，成为了今天所说的塞迈雷迪正则性引理。这个引理在图论中有着非常广泛的应用，甚至可以说，这个引理比塞迈雷迪定理本身更为重要。

但弗斯滕伯格在这个定理中却看到了别的东西。在讲座结束之后不久，他就给讲者发了一封电子邮件：“我可能找到了这个定理的另一种证明。”他在塞迈雷迪定理中看到的，自然是动力系统。

我们考虑所有由整数组成的集合，这些集合组成了一个状态空间。对于某个集合A，如果将其中的每个整数都加上1，我们就得到了另一个集合，这种变换又叫平移变换。然后弗斯滕伯格利用平移变换，定义了有关整数集合的一些保测动力系统，而塞迈雷迪定理就相当于断言这些保测动力系统假以时日必定会以特定的方式多次“回归”初始状态，就像庞加莱复现定理所证明的那样。接下来，弗斯滕伯格洞察到，这个结论不仅对于这些有关整数集合的保测动力系统成立，而且对更广泛的双射保测动力系统也成立。于是他将庞加莱复现定理推广到多次回归的情况，证明了所谓的“弗斯滕伯格多次复现定理”，由此也就推出了塞迈雷迪定理。

弗斯滕伯格对于他的多次复现定理的证明也很耐人寻味。首先，定理中的动力系统可以分解为遍历系统，所以我们可以利用遍历理论的工具来研究这一点。虽然遍历系统数不胜数，但它们之所以拥有遍历这一性质，基本上出于两种原因：要么系统本身几乎是周期性的，也就是说，经过一定时间之后，系统中的状态会几乎回到原始状态，但却有一点点偏差，日积月累的话，靠这种偏差就能逼近所有状态；要么系统本身就处于混沌之中，不同部分的状态在经过一些时间之后就会均匀地混合在一起无法区分，而每个状态也会很快“忘记”自己的起点，和光同尘。虽然本质并不相同，但这两类遍历系统中都存在多次复现的现象。然后弗斯滕伯格证明了，他考虑的动力系统中必定包含前面其中一种遍历系统，从而也会有多次复现的现象。这个证明就很有拉姆齐理论的风格：无论动力系统如何复杂混乱，都能从中找出拥有特定规律的一部分。

弗斯滕伯格的证明的意义在于，它打开了利用动力系统的工具来研究困难组合问题的大门。塞迈雷迪原本的证明虽然很有意义，但却非常艰深，用到了复杂的技术，不容易推广到更普遍的情况。但弗斯滕伯格的证明，虽然用到了看似复杂的动力系统，但总体而言更直观更容易理解，也容易推广。之后不久，弗斯滕伯格和他的合作者就将这个动力系统证明进行了各种各样的推广，获得了与塞迈雷迪定理类似的数个更为强大的结论。在弗斯滕伯格等人的开拓下，利用遍历理论对类似问题的研究已经成为了一门名为“遍历拉姆齐理论”的分支，也结出了相当的成果。

虽然弗斯滕伯格除此以外还有不少其他方向的研究，但他在整数中看到动力系统的这一洞察，将原本属于连续的方法延伸到了离散，用全新的视角得出了出人意料而又困难的结论，并且他开辟的这条道路仍然有着大量的问题等待探索。可以说，弗斯滕伯格的这项成果，属于数学中第一流的贡献。

马尔古利斯：代数中的遍历系统

另一位获奖者格里戈里·马尔古利斯的运气相对来说稍微好一些。他也是犹太人，然而他出生于1946年苏联的莫斯科，虽然也被歧视，但起码性命无虞。马尔古利斯很早就展露出了数学天赋，16岁时参加国际数学奥林匹克就获得了银奖，之后也进入了在数学方面最负盛名的莫斯科国立大学就读。因为是犹太人，所以马尔古利斯想必也攻破了在入学口试中专门用于防止犹太人入学的“棺材问题”，也就是有着初等解答但却极端困难的问题。他居然能够作为一名犹太人入读莫斯科国立大学，只能说明他的数学天赋实在是出类拔萃。

在博士期间，马尔古利斯师从动力系统专家雅科夫·西奈（Yakov Sinai，2014年获阿贝尔奖），动力系统也就成了他研究的主线。但他研究的并不算是传统的动力系统理论，而是动力系统理论在代数领域的应用。

我们身边的许多东西都有着令人惊异的对称性。五瓣的梅花旋转72度后，与原来丝毫不差；六芒的雪花，如果将它旋转60度，或者沿着某根主轴翻到另一面，也保持与原来几乎相同的形态；光盘更是无论如何旋转，几乎都无法与原本的状态区分开来。所有这些东西，如果对它们执行某些特定的动作，那么得到的结果与原来的状态没有区别，这就是它们对称性的一种体现。对称性越高，符合这种条件的动作也越多。我们会觉得轮胎比梅花更对称，因为旋转梅花时，如果角度不是72的倍数，那么花瓣就会错位，但光盘无论旋转什么角度都几乎不变。从这种对称性抽象而来的数学对象就是群，那些动作就是群的元素，而群论就是通过群这种抽象结构来研究种种对称性的数学分支。

数学中有着各种各样的群，而数学家花了大量的精力来对这些群进行分类。最简单的分类之一就是连续群和离散群。光盘的对称群就是连续的，因为我们可以旋转任何角度，稍微多转一点少转一点，对于光盘来说无关紧要。也就是说，光盘的对称群中的元素是可以连续变化的。另一方面，梅花的对称群就是离散的，要保持形状完全不变，旋转角度就必须是72的倍数，多一点少一点都不行。所以，梅花的对称群中每个元素之间都被远远地分隔开来，这就是它被称为“离散群”的原因。

不同的群之间可以有各种各样的关系，最直白的就是一个群可以包含另一个群，这时我们也说后者是前者的子群。比如说光盘的对称群就包含了梅花的对称群，因为梅花的对称群中的元素都是角度各异的旋转，而光盘的对称群包含了所有角度的旋转，自然也包含了梅花的对称群中的所有元素。容易发现，连续群中可以包含离散群，但离散群却无法包含连续群。数学家发现，对于某些连续群来说，只需要研究它包含的离散群，就能得出许多关于连续群本身的重要性质。马尔古利斯的研究就处于这个方向，而他研究的群，专业术语里被称为“半单李群”，而其中包含的离散群被称为“格子群”。

但这些群跟动力系统又有什么关系呢？

之前提到，群可以看成保持某些结构不变的操作组成的集合，但这个结构完全可以是这个群本身！我们可以将整个群看成一个状态空间，而群里的元素就是状态。但群里的元素也可以看作对状态空间的变换。于是，我们可以通过选取合适的元素作为变换，在整个群中定义出各种各样的动力系统。此外，在群中也可以定义某种特定的“容积”，也就是测度，使得所有这些通过群里元素定义的动力系统都是保测动力系统。从这里开始，遍历理论就能派上用场了。

在马尔古利斯之前的数学家就已经意识到，通过某些特定的连续动力系统的性质，就能推测出连续群的各种性质，而马尔古利斯在前人的基础上更进一步，利用动力系统以及概率论的方法，证明了半单李群格子群的许多重要结论。其中最重要的大概是他在1975年证明的“超刚性定理”，刻画了半单李群中被称为“算术格子群”的一类有着重大意义的格子群，还有他在1978年证明的“正规子群定理”，刻画了半单李群格子群的重要性质。正因为做出了这些重要的工作，他被选为1978年菲尔兹奖的四位获奖者之一。

但他并没有亲自领到这一奖项。

1978年，冷战正酣。虽然几年前美苏和欧洲各国签订了赫尔辛基条约，在欧洲换得了暂时的和缓，但很快双方关系又因为其他冲突继续恶化。在当时的苏联，出境必须预先向政府报批，而马尔古利斯未能获批去往赫尔辛基参加国际数学家大会。这也许是苏联的传统，马尔古利斯的前辈谢尔盖·诺维科夫（Sergei Novikov）在八年前也获得了菲尔兹奖，同样由于未受苏联政府批准出境而无法出席领奖。只有到12年后的1990年，苏联已然苟延残喘时，他们的后辈弗拉基米尔·德林费尔德（Vladmir Drinfeld）才能够亲身领到属于他的菲尔兹奖。

而即使已然跻身顶尖数学家的行列，这也没有给马尔古利斯带来多少好处，因为他是苏联的犹太人。在博士毕业之后，尽管已是同龄人中的佼佼者，他却无法在苏联数学水平最高的莫斯科国立大学找到教职，只能就职于信息通讯问题研究所（Institute for Information Transmission Problems）。这个研究所的名字，一看就知道与马尔古利斯所研究的数学相去甚远。

但这也许并不完全是一件坏事。马尔古利斯在研究所的同事主要研究计算机科学。有一次，他们向马尔古利斯提到了扩展图的概念。扩展图是一种特殊的组合对象，在复杂度理论中，它可以将少数几个随机比特扩增为一大批随机性足够强的伪随机数来提供给随机算法使用。因此，研究者会利用它将某些随机算法“去随机化”，将其转变为确定性的算法。但在1973年，人们只知道扩展图必定存在，但却没有人知道如何明确构造一系列的扩展图。马尔古利斯听到这个问题之后不久，就找到了一个明确的构造回答了这一问题，而他的构造利用了他在研究半单李群格子群时用到的所谓“卡日丹（Kazhdan）性质(T)”，一个牵涉代数表示论的性质。深奥的代数结论带来的重要构造，在计算机科学的历史上可以说凤毛麟角，而这一跨界行为也展现出马尔古利斯解决各种问题的能力。

然而，马尔古利斯之后的跨界更为惊人。

我们在中学都学过多项式，比如说xy+yz+xz就是一个三元二次多项式。不仅如此，因为它的每一项都是二次的，所以我们也说它是一个齐次的多项式。数学家猜想，对于至少包含三个变量的实数多项式，假设它的取值可以为正也可以为负，而且所有系数同时除以任何实数都不会同时得到有理数的话，那么随便选取一个实数x，都能找到一些整数，将它们代入多项式之后得到的值可以离x要多近有多近。这就是所谓的奥本海姆猜想，它属于“丢番图逼近”这一领域，也就是关于用整数或者有理数通过不同的方法来逼近任意实数的研究，属于数论的范畴。

一般来说，丢番图逼近的问题都不怎么容易，通常会用到分析数论或者代数数论的深奥结论。奥本海姆猜想也不例外，但那些常用方法在这里却碰到了死胡同。但在1987年，马尔古利斯利用遍历理论漂亮地证明了这个猜想。他首先观察到一个已知的结果：奥本海姆猜想等价于有关某个特殊的半单李群格子群的断言。然后通过之前对半单李群格子群的研究，他找到了这个断言与某些遍历系统之间的关系，从而利用遍历理论中的方法得出了证明。

马尔古利斯的这一证明，给丢番图逼近这一领域引入了全新的方法。自此之后，人们开始关注动力系统与丢番图逼近之间的关系。而更重要的是，马尔古利斯利用遍历理论的方式非常新颖，从中发展出了一门名为齐性动力系统的全新分支，并且由此得到了大量与数论等其他领域相关的重要结果。

与弗斯滕伯格一样，马尔古利斯除此之外还有众多重要的工作，但他利用动力系统的视角去解决代数问题，然后又在数论问题中觉察到代数结构，然后再利用动力系统与代数结构之间的联系去解决数论问题的这一洞察力实在令人赞叹，不仅在数学的不同分支之间看到了相似的结构，而且还能活用这种相似性来解决困难的问题，甚至连解决办法本身都引出了更深入的研究方向。毫无疑问，对于数学来说，这同样是第一流的贡献。

顺带一提，马尔古利斯在获得菲尔兹奖之后，虽然职位和待遇一时也没有什么变化，但出国访问比较容易获得批准了。之后他经常出国访问，在苏联解体之后也很快移居到了美国，就任耶鲁大学的教授，直到退休。

结语

纵观弗斯滕伯格和马尔古利斯的工作，可以说，他们各自的工作将动力系统这一原本更偏向于概率论的数学分支，与代数、组合、数论等看似风马牛不相及的数学分支联系了起来，由此创造了新的数学分支。他们证明的结论不仅重要，而且富有洞察性，为数学开辟了新的道路。两人都曾获得沃尔夫数学奖，这次同时获得沃尔夫奖这一数学界的终身成就奖，完完全全实至名归。

数学，是研究抽象结构及其之间关系的学科。虽然数学被人为分成了无数的分支，不同的数学分支有着不同的方法论，对抽象结构的着眼点也各不相同，但抽象结构本身却并不专属于任何一个分支，而是可以在截然不同的分支之中同时出现。然而，只有那些智者，才能洞察那些繁杂的数学分支，发现它们之中有着相同的抽象结构，从而将一个分支的方法，通过同一个抽象结构，用于解决另一个分支的问题。在科研越来越细化的今天，这种能力越发珍贵。

参考文献

1. De la Salle, Mikael, “Raconte moi… la propriété (T) “, Gazette des Mathématiciens, Société Mathématique de France, 2016.
2. Dinur, Irit, “The PCP theorem by gap amplification” (PDF), Journal of the ACM, 54 (3): 12–es. 2007.
3. Eskin, Alex, “Unipotent Flows and Applications”, Clay Mathematics Proceedings, Volume 10. 2010.
4. Furstenberg, Hillel; Katznelson, Yitzhak; Ornstein, Donald Samuel. “The ergodic theoretical proof of Szemerédi’s theorem”. Bull. Amer. Math. Soc. 7 (3): 527–552. 1982.
5. O’Connor, John J.; Robertson, Edmund F., “Grigory Margulis”, MacTutor History of Mathematics archive, University of St Andrews.
6. O’Connor, John J.; Robertson, Edmund F., “Hillel Furstenberg”, MacTutor History of Mathematics archive, University of St Andrews.
7. “Furstenberg and Smale Receive 2006–2007 Wolf Prize” (PDF). Notices of the American Mathematical Society. 54 (4): 631–632. 2007.
8. “A biography of Grigory Margulis”. The Abel Prize. Retrieved 2020-03-22.
9. “A biography of Hillel Furstenberg”. The Abel Prize. Retrieved 2020-03-22.
10. “Citation by the Abel Committee for the Abel Prize 2020”. The Abel Prize. Retrieved 2020-04-02.
11. “Ergodic hypothesis”. Wikipedia. Retrieved 2020-04-02.
12. “Ergodic theory”. Wikipedia. Retrieved 2020-04-02.
13. “Grigory Margulis”. Wikipedia. Retrieved 2020-04-02.
14. “Hillel Furstenberg”. Wikipedia. Retrieved 2020-04-02.